Solution: 2013 Fall Midterm - 12

Author: Pat Morin

Question

Consider the recursive algorithm $\Fib$, which takes as input an integer $n \geq 0$:

$\mathbf{Algorithm}\ \Fib(n)\mathrm{:}$
$\mathbf{if}\ n = 0\ \mathrm{or}\ n = 1$
$\mathbf{then}\ f = n$
$\mathbf{else}\ f = \Fib(n - 1) + \Fib(n - 2)$
$\mathbf{endif};$
$\mathbf{return}\ f$

When running $ FIB(5) $, how many calls are there to $ FIB(2) $?

(a)

$3$

(b)

$1$

(c)

$2$

(d)

$4$

Solution

We can draw a recursive tree to see how many calls there are to $ FIB(2) $

The best way to do this is to draw it out

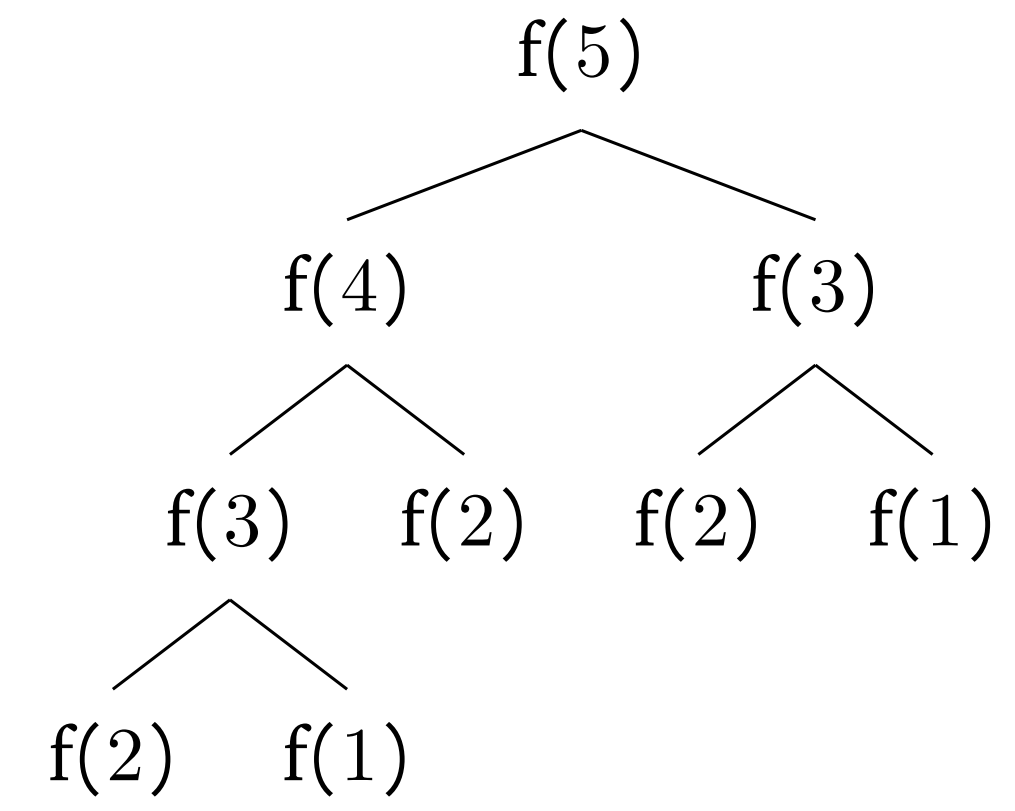
As can be seen, $FIB(2)$ is called 8 times