Solution: 2013 Fall Midterm - 13

Author: Pat Morin

Question

Consider the recursive algorithm $\Fib$, which takes as input an integer $n \geq 0$:

$\mathbf{Algorithm}\ \Fib(n)\mathrm{:}$
$\mathbf{if}\ n = 0\ \mathrm{or}\ n = 1$
$\mathbf{then}\ f = n$
$\mathbf{else}\ f = \Fib(n - 1) + \Fib(n - 2)$
$\mathbf{endif};$
$\mathbf{return}\ f$

For $ n \geq 2 $, run algorithm $ FIB(n)$ and let $ a_n $ be the number of times that $ FIB(0) $ is called.

(a)

$a_n = f_n - 1$

(b)

$a_n = f_{n+1}$

(c)

$a_n = f_{n-1}$

(d)

$a_n = f_n$

Solution

We can draw a recursive tree to see how many calls there are to $ FIB(0) $

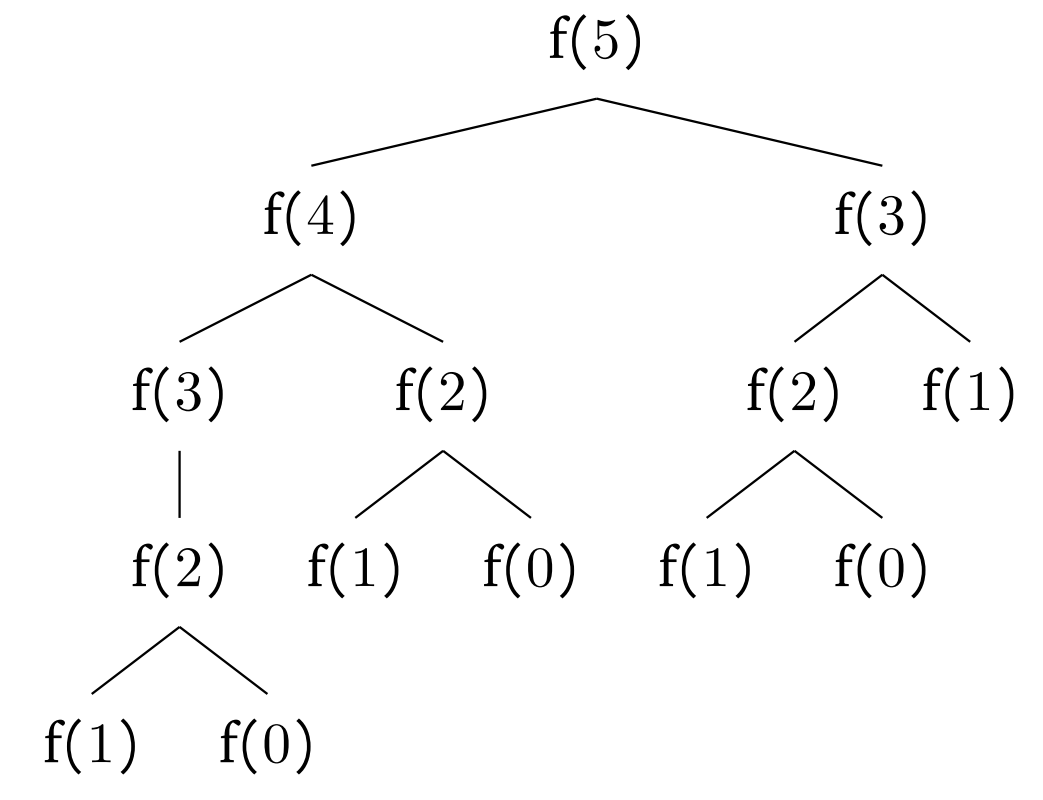
As can be seen, $ FIB(0) $ is called 4 times, which corresponds to $f_{n-1} = f_{5-1} = f_{4}$