Solution: 2015 Winter Final - 9

Author: Michiel Smid

Question

Consider the recursive algorithm $\Fib$, which takes as input an integer $n \geq 0$:

$\mathbf{Algorithm}\ \Fib(n)\mathrm{:}$
$\mathbf{if}\ n = 0\ \mathrm{or}\ n = 1$
$\mathbf{then}\ f = n$
$\mathbf{else}\ f = \Fib(n - 1) + \Fib(n - 2)$
$\mathbf{endif};$
$\mathbf{return}\ f$

If we run algorithm $\Fib(77)$, how many calls are there to $\Fib(73)$?

(a)

(b)

(c)

(d)

Solution

Let’s draw a recursive tree to find out how many calls there are to $FIB(73)$ when we run $FIB(77)$.

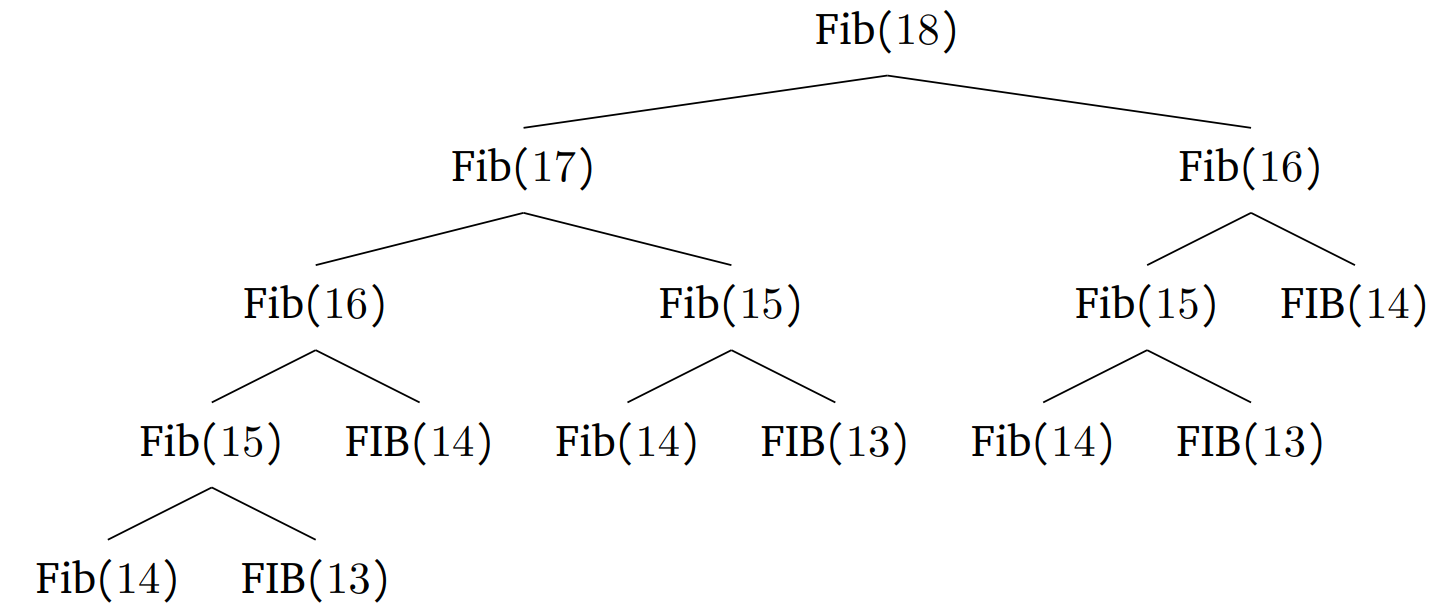
As can be seen, there are 5 calls to $FIB(73)$ when we run $FIB(77)$.