Solution: 2016 Fall Final - 14

Author: Michiel Smid

Question

We flip a fair coin three times; these flips are independent of each other. These three coin flips give us a sequence of length three, where each symbol is $H$ or $T$. Define the events (recall that 0 is even):

A = "the number of $H$ in the sequence is even",
B = "the sequence contains at least two consecutive $H$'s".

Which of the following is true?

(a)

The events $A$ and $B$ are independent.

(b)

None of the above.

(c)

The events $A$ and $B$ are not independent.

Solution

For anything less than 5 flips, I honestly just draw a tree diagram to find the answer

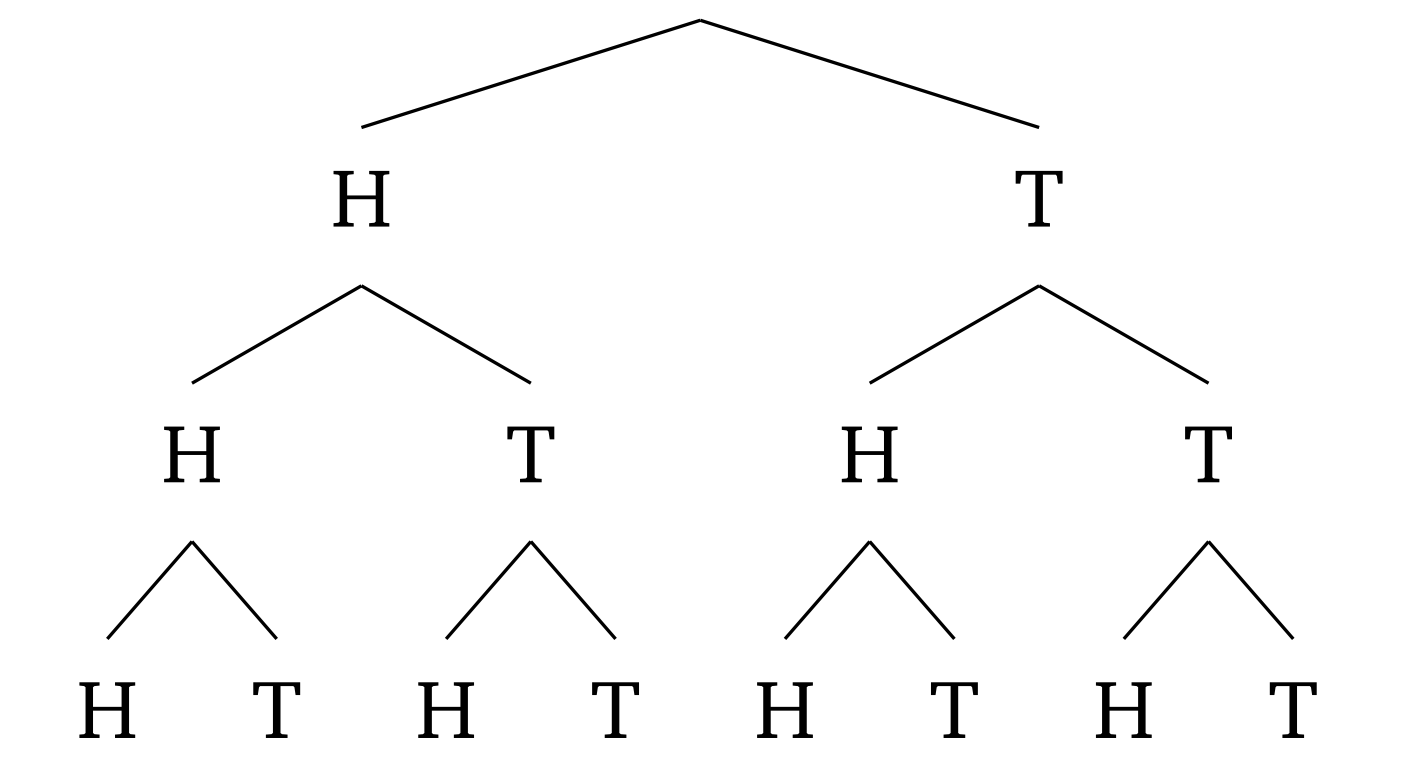
Let's determine S
S is the set of all possible outcomes of the 3 coin flips
$ |S| = 2^3 = 8$
Let's determine A
A occurs when we either get 0 or 2 heads
$ |A| = 4 $
$ Pr(A) = \frac{4}{8} = \frac{1}{2} $
Let's determine B
B occurs when we get 2 or 3 heads
$ |B| = 3 $
$ Pr(B) = \frac{3}{8} $
Let's determine $ A \cap B $
$ |A \cap B| = 2 $
$ Pr(A \cap B) = \frac{2}{8} = \frac{1}{4} $

Now, let’s check if A and B are independent

$ Pr(A \cap B) = Pr(A) \cdot Pr(B) $

$ \frac{1}{4} = \frac{1}{2} \cdot \frac{3}{8} $

$ \frac{1}{4} = \frac{3}{16} $

Since the equation is false, A and B are not independent.