Solution: 2017 Fall Final - 15
Author: Michiel SmidQuestion
You flip a fair coin three times; these three flips are independent. Define the events
- A = "the first two flips both result in heads",
- B = "there are at least two heads in the sequence of three flips".
(a)
The events $A$ and $B$ are not independent.
(b)
The events $A$ and $B$ are independent.
(c)
None of the above.
Solution
Draw out a tree
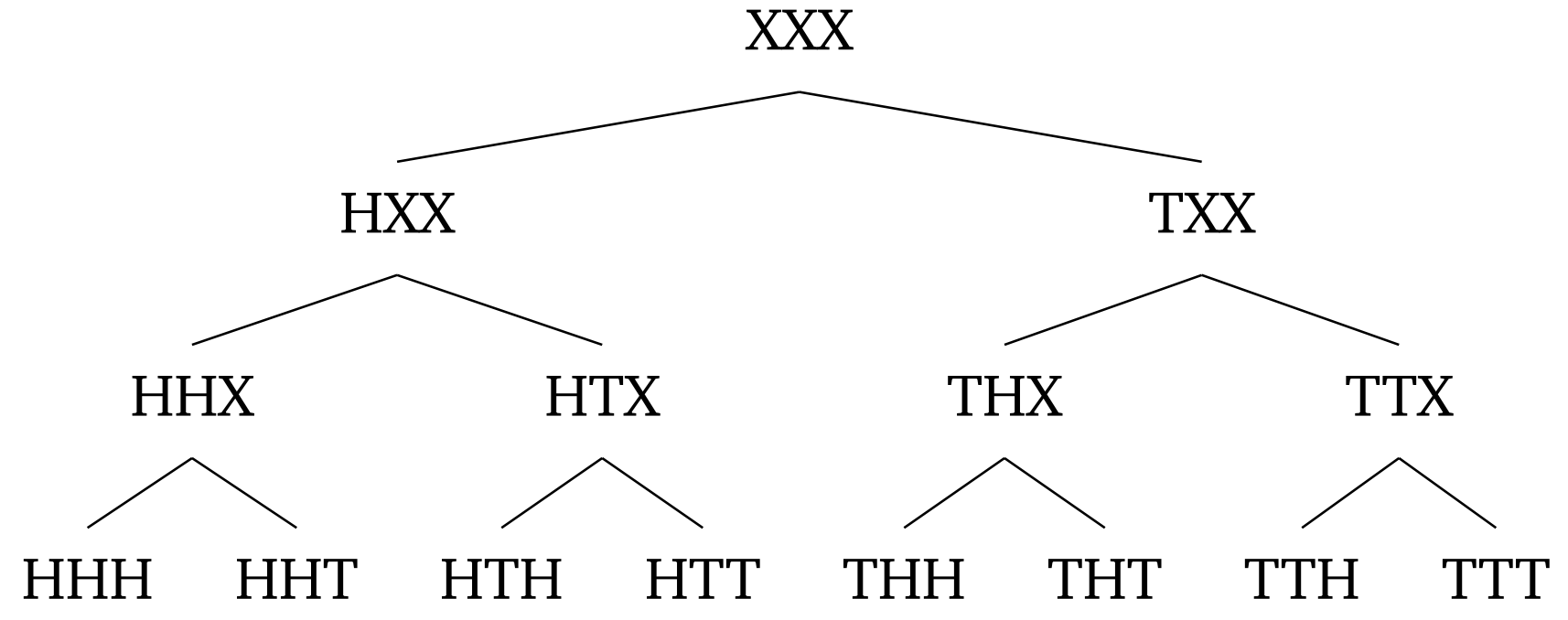
- Let's determine A
$ { (HHH), (HHT) } $
$ |A| = 2 $
$ Pr(A) = \frac{2}{8} $ - Let's determine B
$ { (HHH), (HHT), (HTH), (THH) } $
$ |B| = 4 $
$ Pr(B) = \frac{4}{8} $ - Let's determine $ A \cap B $
$ { (HHH), (HHT) } $
$ |A \cap B| = 2 $
$ Pr(A \cap B) = \frac{2}{8} $
Now, let’s check if A and B are independent
$ Pr(A \cap B) = Pr(A) \cdot Pr(B) $
$ \frac{2}{8} = \frac{2}{8} \cdot \frac{4}{8} $
$ \frac{2}{8} = \frac{1}{4} \cdot \frac{1}{2} $
$ \frac{2}{8} = \frac{1}{8} $
Since the equation is false, A and B are not independent.