$\newcommand{\Fib}{{\rm F \scriptsize IB}}$
Consider the following recursive algorithm $\Fib$, which takes as input an integer $n \geq 0$:
$\mathbf{Algorithm}\ \Fib(n)\mathrm{:}$
$\mathbf{if}\ n = 0\ \mathrm{or}\ n = 1$
$\mathbf{then}\ f = n$
$\mathbf{else}\ f = \Fib(n - 1) + \Fib(n - 2)$
$\mathbf{endif};$
$\mathbf{return}\ f$
When running $\Fib(9)$, how many calls are there to $\Fib(4)$?
a) 6
b) 7
c) 8
d) 9
Solution: 2014 Fall Midterm - 12
Author: Michiel SmidQuestion
$\newcommand{\Fib}{{\rm F \scriptsize IB}}$
Consider the following recursive algorithm $\Fib$, which takes as input an
integer $n \geq 0$:
$\mathbf{Algorithm}\ \Fib(n)\mathrm{:}$
$\mathbf{if}\ n = 0\ \mathrm{or}\ n = 1$
$\mathbf{then}\ f = n$
$\mathbf{else}\ f = \Fib(n - 1) + \Fib(n - 2)$
$\mathbf{endif};$
$\mathbf{return}\ f$
(a)
8
(b)
6
(c)
7
(d)
9
Solution
The best way to do this is to draw it out
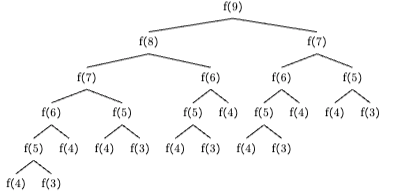
As can be seen, $f(4)$ is called 8 times
