You flip a fair coin 5 times. Define the events $$ A = \text{“the number of heads is odd”} $$ and $$ B = \text{“the number of tails is even”} $$ Which of the following is true?
a) $\Pr(A) = \Pr(B)$
b) $\Pr(A) < \Pr(B)$
c) $\Pr(A) > \Pr(B)$
Solution: 2014 Fall Midterm - 15
Author: Michiel SmidQuestion
You flip a fair coin 5 times. Define the events
- A = "the number of heads is odd"
- B = "the number of tails is even".
(a)
$\Pr(A) > \Pr(B)$
(b)
$\Pr(A) < \Pr(B)$
(c)
$\Pr(A) = \Pr(B)$
Solution
We can draw this out for clarification with a smaller example of 3 flips:
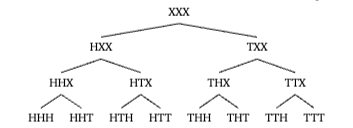
Here, there are 4 possibilities of even tails out of 8 possibilities
There are 4 possibilities of even heads out of 8 possibilities
$Pr(A)=1/2$
$Pr(B)=1/2$
(a) is correct
