Solution: 2018 Fall Midterm - 14
Author: Michiel SmidQuestion
$\newcommand{\Fart}{{\rm F {\scriptsize ART}}}
\newcommand{\elsesp}{\phantom{\mathbf{else}\ }}
\newcommand{\thensp}{\phantom{\mathbf{then}\ }}$
Consider the recursive algorithm $\Fart$, which takes as input an integer $n \geq 0$:
$\mathbf{Algorithm}\ \Fart(n)\mathrm{:}$
$\mathbf{if}\ n = 0\ \mathrm{or}\ n = 1$
$\mathbf{then}\ \text{eat one can of beans}$
$\mathbf{else}\ \mathbf{if}\ n\ \mathrm{is}\ \mathrm{even}$
$\elsesp \mathbf{then}\ \text{fart once};$
$\elsesp \thensp \Fart \left( n \middle/ 2 \right)$
$\elsesp \mathbf{else}\ \Fart(n + 1);$
$\elsesp \elsesp \text{fart once};$
$\elsesp \elsesp \Fart(n - 1)$
$\elsesp \mathbf{endif};$
$\mathbf{endif}$
(a)
12
(b)
11
(c)
13
(d)
14
Solution
Every call other than Fart$(1)$ and Fart$(0)$ results in a fart.
Let’s draw a recursive tree to see how many times the fart procedure is called.
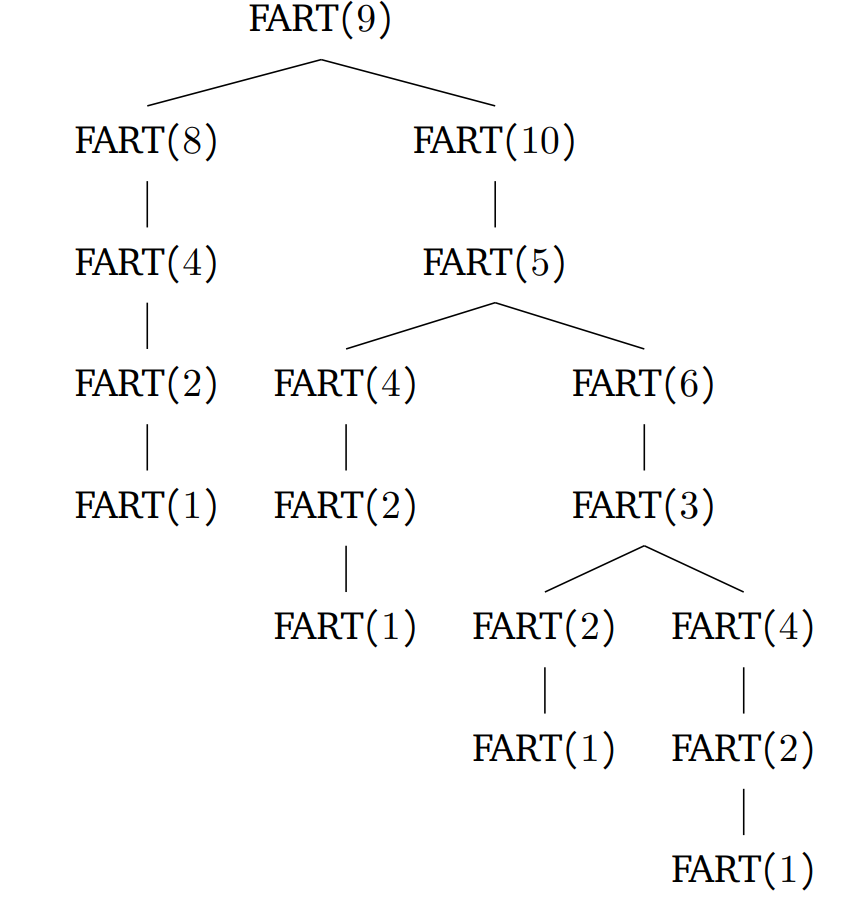
Calls above Fart$(1)$ and Fart$(0)$ result in a total of 13 farts.
