Solution: 2019 Fall Final - 21

Author: Michiel Smid

Question

Let $n \geq 2$ be an integer. Consider a string $c_1,c_2,...,c_n$ of length $n$, in which each character $c_i$ is a uniformly random element of the set $\{1,2,3\}$ (independently of all other characters). Consider the random variable $X$ whose value is the number of indices $i \in \{1,...,n - 1\}$ for which the product $c_i \cdot c_{i + 1}$ is odd.

What is the expected value $\mathbb{E}(X)$ of the random variable $X$?

Hint: Use indicator random variables.

(a)

$\frac{4}{9} \cdot n$

(b)

$\frac{2}{3} \cdot (n - 1)$

(c)

$\frac{2}{3} \cdot n$

(d)

$\frac{4}{9} \cdot (n - 1)$

Solution

Let $X_i$ be 1 if the product $c_i \cdot c_{i+1}$ is odd

Let A be the event that the product $c_i \cdot c_{i+1}$ is odd

Let’s draw a multiplication table, baby

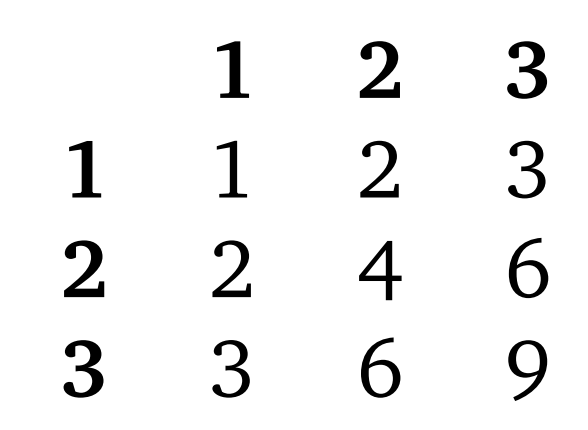
There are 3 odd products: 3, 6, 9

Out of 9 events, the event of an odd product occurs 4 times

$ Pr(A) = \frac{4}{9} $

$ E(X) = \sum_{k=1}^{n-1} Pr(X_i = 1) $

$ E(X) = \sum_{k=1}^{n-1} Pr(A) $

$ E(X) = (n-1) \cdot \frac{4}{9} $